10-bit log vs 12-bit linear

I have written on the subject of linear vs. log encoding before, but the issue keeps coming up as more users attempt to compare REDCODE to CineForm RAW. While there is plenty of mythology around most of what RED does, the smoke around REDCODE is clearing, so comparisons will and are being made between the only two wavelet based RAW compressors in existence. While I would love to do a head-to-head test starting with the same uncompressed RAW frames, that will be difficult until the Red RAWPORT is ready. So this article does not attempt to do a quality comparison between REDCODE and CineForm RAW; instead I hope to reveal the impacts of 10-bit log (used by CineForm RAW) vs. 12-bit linear (publicly disclosed as used by REDCODE) as it relates to lossy* compression.

* Lossy - sounds bad doesn't it? But even visually lossless compression is not mathematically identical to the original. To reliably achieve image compression above about 2:1, a lossy compression is required.

In the cases of both CineForm RAW and REDCODE compression, the decision to apply a log or linear curve is a design choice, not a software/hardware limitation. CineForm compression delivers up to 12-bit precision (see info on CineForm 444), so 12-bit linear compression with CineForm RAW is certainly an option. Similarly, REDCODE could have chosen to compress 10-bit log; both algorithms could compress 12-bit log with suitable source data. So while there are marketing advantages to numbers 12 over 10, and similarly some marketing advantage to Log over Linear (too often incorrectly associated with "video"), there are real world quality impacts that we want to explore in more detail.

* For those wanting a refresher on Log vs. Linear vs. Video Gamma, please see this ProLost blog entry by Stu Maschwitz.

For this post I tried doing a little research on log vs. linear compression impacts on human visual artifacts, but I didn't get very far. Almost all compression analysis for video and still imagery is done on 8-bit data that already has some display curve applied (typically a 2.2 gamma curve.) There are good reasons for this; when testing for the visual impact of compression, you typically test using the target display presentation format, i.e. resolution, gamma curve and bit-depth match the output display. For digital cinematography you can't assume an output curve, as you are shooting to allow for a wide range of post processing before it is delivered to a wide variety of display types with differing curves - there is no way of knowing your output delivery curve at shoot time.

There is an assumption in the above paragraph that compression introduces less distortion when applied to the output curve. We see this every time we switch on the television or download a video; the compression is applied to the final color and gamma corrected sequence. An alternative approach might be to encode with one curve, and have the decoder output to another, yet we don't see this much, certainly never in distribution formats. All this gets into the hairy subject of human visual modeling and the suppression of noise in the shadow regions of the image. The reason common curves like 2.2 gamma are applied for distribution derives from the classic book Video Demystified by Keith Jack :

...[has the] advantage in combatting noise, as the eye is approximately equally sensitive to equally relative intensity changes.

There is a lot in that short sentence. Starting with the second part about the eye's sensitivity, light that changes intensity from 2 to 4 (this could number candles or photons per unit time) is perceived the same relative to increasing brightness from 50 to 100 - each is perceived as getting approximately twice as bright. Now think of the analog broadcast days, where the channel is very sensitive to noise. Noise is an additive function, so noise of + or - 1 in this example could result in reception of 1 to 5 and 49 to 101. The noise in the brighter image will not be seen, yet the darker values/image are significantly distorted. Gamma-encoding the source (2 to 4) would produce something like 28 to 38, and 50 to 100 would be transmitted as 122 to 167 (using 2.2 gamma.) So even with the same noise added to the gamma-corrected value, the final displayed value (the display device reverses the gamma) would be 1.8 to 4.1 and 49.5 100.5. These resulting numbers greatly improve the darker regions of the image without compromising the highlights.

So what does all this have to with digital image compression? The introduction of compression is equivalent to the additive noise effect I just discussed. While compression artifacts are not as random as in the analog world, they are additive in the same way, so the impact to shadow regions of the image is the same. Some might think you can design compression technology that compresses the shadows less - sounds like a great idea - yet that already exists, adding a curve to pre-emphasize the shadows does exactly this. Let's look at why compression noise is additive; if you don't care about that skip to the next paragraph.

Examining why compression distortion is additive, just like analog noise, requires a base understanding of image compression. Visual compression technologies like DCT and Wavelets divide the pixel data by frequency, where low frequency data is more important to the eye than high frequency data, which is exploited to reduce the amount of data transmitted. The simplest compression example is when we transmit the average values (low frequency = (v1+v2)/2) of adjacent pixels, at full precision, and also transmit the difference of the adjacent pixels (high frequency = (v2-v1)/2) with less precision (compression through quantization). That is the basis of DCT and Wavelets; differences between the two arise in how the low and high frequency values are calculated. Let's reconsider our original bright pairs 2,4 and 50,100; imagine they are adjacent pixel values. Low pass data is (2+4)/2 = 3, and (50+100)/2 = 75; the high pass data is (4-2)/2 = 1, and (100-50)/2 = 25. If we transmit the data with quantization (no lossy compression), the original image can be perfectly reconstructed as 3-1=2, 3+1=4 and 75-25=50, 75+25=100. Now to model compression let's quantize the high frequency components by 2. With decimal points rounded off for compression we get (4-2 )/(2*2) = 0, and (100-50)/(2*2) = 12, now the reconstructed image is 3,3 and 51,99 (e.g. 75-12*2 = 51, 75+12*2 = 99.) All the shadow detail has been lost, yet the highlights are visually lossless. Distortion due to quantization is +/-1 in the shadows and also +/-1 in the highlights - quantization impacts dark and light regions equally, just as in analog noise. Doing the same compression with curved data (28,38 and 122,167) yields reconstructed values as 29,37 and 122,166 which is then displayed as 2.1,3.6 and 50.4,99.2, leaving significantly more shadow detail. This example shows is why compression is typically applied to curved data.

If linear is so poor with shadows, wouldn't the optimum curve have each doubling of light (each stop,) be represented with the same amount of precision? This seems completely reasonable. Instead of storing linear light, each uses the values 2048 to 4095 to represent the last stop of light, so why not divide the available values amongst the number of stops the camera can shoot. Let's say (for simple math) your camera has around 10-stops of latitude, that would place around 400 levels per stop or 100 levels per stop in 10-bit. Now in your creative post-production color grading, it doesn't matter whether you use the top five stops or the bottom five to create a contrasty image - the quality should be the same. It turns out we don't have an ideal world, so while moving compression of the top stop of 2048-4095 down to around 900-1000 (10-bit) is fine, we find that expanding the 10th stop values of 0 to 8 up to 0 to 100, while preserving all the shadow detail, also preserves (beautifully) all the details of sensor noise, which is always present, and which is difficult to compress. It may also be obvious that expanding the "8" value to "100" doesn't gains you 100 discrete levels in the last stop -- for that you would need the currently impossible, 16-bit sensor with about 90dB SNR. So while these new cameras claim 11-stops, don't go digging too far into the shadows.

* NOTE: 400 levels per stop using 12-bit precision sounds 4 times better than using 10-bit. However, once you compress the image the difference mostly go away. To achieve the same data rate the 12-bit encoder has to quantize its data 4 times as much. The 12-bit compression only really starts to pay off with very little compression, say between 5:1 and 2:1.

The curve that is applied is a compromise between compression noise immunity and coupling too much sensor noise into the output signal. As a result there is no standard curve for digital acquisition, as the individual sensor characteristics and bitrate of the acquisition compression all play a part when designing a curve. This goes for the Thompson Viper Filmstream curve recording to an HDCAM-SR deck and also to an SI-2K recording to CineForm RAW -- the curves are different. But as long as the curve is known, it is reversible, allowing linear reconstruction as/when needed. So the curve is just a pre-filter for optimum quality compression.

Now for some real world images. To clearly demonstrate this issue I started with an uncompressed image that I shot RAW with my 6MPixels Pentax *IST-D. Using Photoshop I produced a 16-bit linear TIFF source for After Effects. Here is the source image displayed as linear without any gamma correction.



Here the source is corrected with a 2.2 gamma for the display, looking very much like the shooting environment.


To help showcase the shadow distortion, I zoomed in on a dark region that has some worthy detail I then applied a little "creative" addition by increasing the gamma to 3.0 (from 2.2) to enhance the shadow detail. Below is the same image encoded using linear to 4:4:4 using the worst quality settings for CineForm and JPEG2000. (I used the worst (highest compression) setting to help enhance compression artifacts -- as bitrates increase the artifacts diminish). I would have preferred to only use JPEG2000 (I don't like running CineForm at this low quality), however the AE implementation of J2K via QuickTime is only 8-bit so it introduces banding as well as linear compression issues. You can see there is a different look to JPEG2000 and CineForm when heavily compressed, yet they both show problems with the shadows with a linear source. With CineForm set to Low and JPEG2000 set to 0 (on the quality level) the output compression ranged between 23:1 and 25:1. The images have their linear output corrected to a gamma of 3.0. Click any image to see them at 1:1 scale.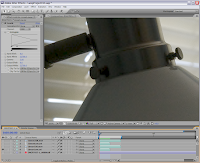

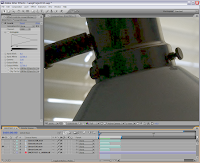While there is plenty of compression artifacts in the dark chrome of the lamp, the white of the lamp shade is showing the noise becoming very blotchy as the natural detail/texture carried in the noise is lost.

The images below have a Cineon log curve applied before compression. The Cineon curve, while good for film, is not well optimized for digital sources. It sets the black level to 95 and the white to 685, giving you around 9-bits of curve to cover the 12-bit linear source. Yet even still, the results show the benefit of the log encoding. The images below have their Cineon curve reversed and the Levels filter 3.0 gamma applied.

So designing a log curve that is optimized for the camera's sensor and its compression processing will generate superior shadow quality through compression processing than will linear compression, but without visible impact to the highlights. While the quality on the latter images is superior, it is worth noting that the bitrate didn't change more than a couple of percent up or down. Although it's a different topic, this also demonstrates that compression data rate (only) is not a good indicator of image quality.
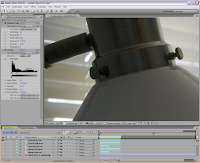
So I don't end the pictorial by only showing heavy compression, here are a couple of log encoded screen shots at 8.8:1 and 5.5:1 compressed; notice at these higher data rates the Cineon log coding looks identical to the 16-bit TIFF source. The bottom line is that properly designed log curves optimized for the camera will provide better resulting images than coding linear data.

The case for Linear:

While I have done my best to make the case for log or gamma encoding before compression, are there any advantages to linear coding in general? Firstly, uncompressed 12-bit does contain more tonal information in the highlights without sacrificing shadows. You would likely store the data as a linear 16-bit TIFF sequence, which will provide very large amounts of data to deal with -- this 6MPixel example at 24fps would be 829 MB/s (for 4K images you'll generate 1+GB/s.) If your workflow includes uncompressed 10-bit log DPX files, your data rate is still high at 552 MB/s (768MB/s for 4K) so it might seem the difference is small enough to stick with the 12-bit. While mathematically you have more data you would likely never see the difference.

Just like uncompressed, compressed linear data has more tonal detail in the last couple stops -- so an overexposed image may do well through compression. Linear encoding can be considered as a curve that emphasizes the highlights as far as the human eye is concerned, so there may some shooting conditions where that emphasis is beneficial. Yet overexposing your digital cameras image lends to unwanted clipping; generally for digital acquisition an under-exposure is preferred.

Linear coding also looks great in mathematical models that measure compression distortion. Algorithms like PSNR and even SSIM interpret curves as producing unwanted distortion (when referencing the linear image), even if the results actually look better with a curve applied. This is one reason I'm careful when using only these measurements when tweaking CineForm codec quality as you are in danger of making an image look better to a computer but not to the final viewer.

Linear compression eats shadow noise - that may be perceived as a good thing. Many have discussed in the Red online forums that wavelets can be used as noise reduction filters - that is true. Unfortunately is it not possible to completely separate noise form detail, some detail will be lost though noise filtering. Noise filtering can help with compression, giving the compressor less to do as a means to reduce the data rate. While noise can be added back, lost information cannot. If you can encode the image including the shadow noise, you provide the most flexibility in post as noise can always be filtered later.

Finally, linear coding is a little easier when performing operations like white balance and color matrix as these operations typically occur in the camera before the curve is applied, yet before the compression stage of all traditional cameras: DV, HDV, DVCPRO-HD, HDCAM, etc. All these camera technologies use curves so that compression to 8-bit still provides good results. In the new RAW cameras, white balance and color matrix operations are delayed into the post production environment, which is one of the key reasons that makes RAW acquisition so compelling -- improved flexibility through a wider image latitude. If you apply a curve to aide compression you have to remove that curve before you can correctly do white balancing, saturation and linear operations in compositing tools. Now if the curve is customized for the camera, like Viper Filmstream or SI-2K's log curve, downstream tools may not know how to reverse the curve to allow linear processing. This can be a real workflow concern, so vendors like Thompson provide the curves for Viper Filmstream, and with the SI-2K using CineForm RAW the curve management is handled by the decoder, presenting linear upon request.

Note: For those who want to know the curve used by the SI-2K, it is defined by output = Log base 90 (input*89+1).

While converting curved pixel data back to linear for these fundamental color operation does add a small amount of compute time, this is all under-the-hood in the CineForm RAW workflow. Our goal is working towards the most optimized workflow without sacrificing quality. We view curves as one of the elements required for good compression. The black box of our compression includes the input and output curves as needed. If you consider this whole black box, CineForm RAW supports linear input and linear output, but without linear compression artifacts.